C++ Programming GalleryMath and others
Random number generator in C++ (Aleator)
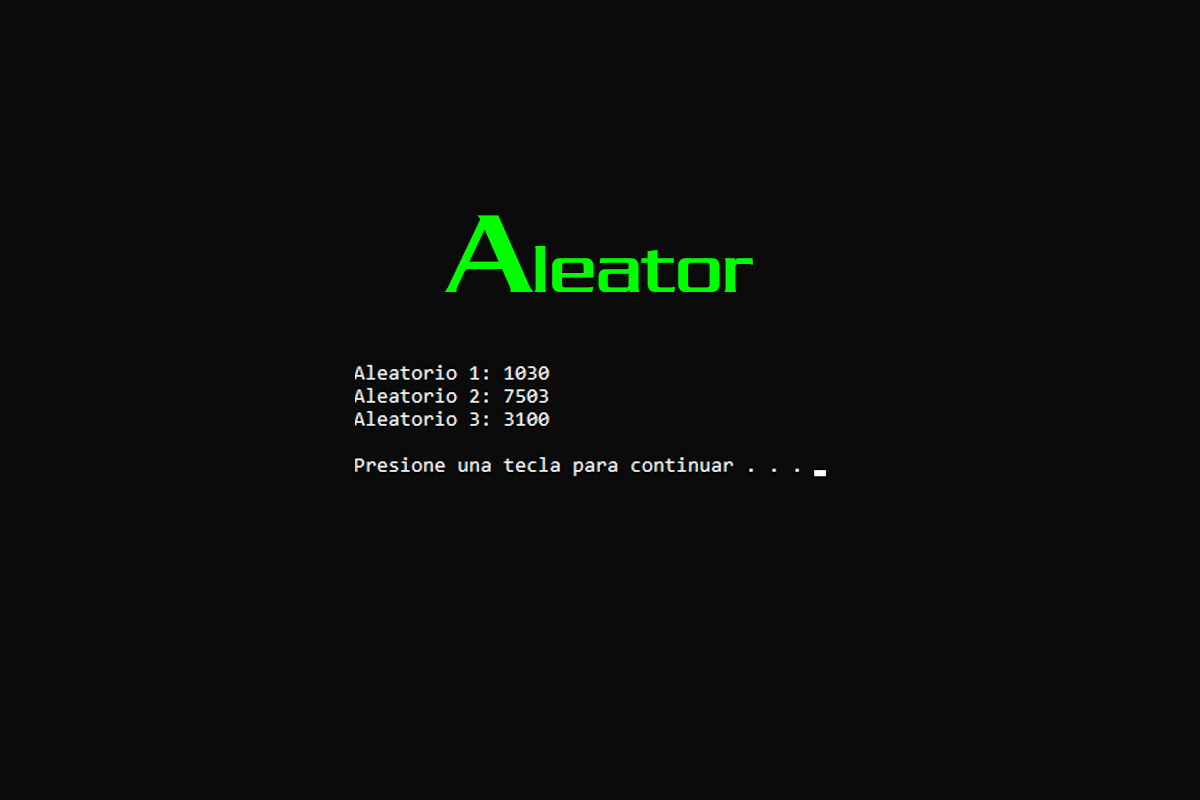
Three different ways to define a function that returns random numbers, in the same style as the random function. This is an excellent way to define random if your compiler does not have the random function (not ANSI C).
Developed by:
YACSHA – Software & Desing, since 1999, Lima – Perú
The World of Chaos – EL MUNDO DEL CAOS – Unlimited Programming
You can DOWNLOAD the SOURCE CODE and executable software for FREE from here:
Join The World of Chaos Developer Community😃
Contribute to the project on Github!HISTORY
- Version 2 – 19-IV-2024
- Update math-and-others\aleator – Porting to VC++ 2017 using winbgi
- Version 1 – 25-V-2001
- First version for Borland C++ 3.1 and Turbo C 3.0